In 1607 Andrea Ghisi, a Venetian nobleman, published a peculiar book entitled Il laberinto del Signor Andrea Ghisi nel qual si contiene una tessitura di due mila ducento sessanta Figure, che aprendolo tre volte, con facilità si può saper qual figura si sia immaginata. The book begins with a dedication to the Prince of Mantua, Francesco Gonzaga (1577-1616), where the author describes his work as an “exercise of idleness”: a recreational activity with no practical purpose, useful to recover energies and restore body and soul.

Me in the Queriniana Library in Brescia (Italy)
In 1610 the London publisher Thomas Purfoot printed its English translation, entitled Wits Laberynth or, the Exercise of Idlenesse containing an artificiall texture of two thousand two hundred and sixtie figures, so placed and disposed, as by the helpe of a briefe Direction for that purpose, you may tell which of them any man thinketh.
In 1616 the book was reprinted in Italy by the Venetian typographer Evangelista Deuchino with the new title Laberinto dato novamente in luce dal Clarissimo Signor Andrea Ghisi, nobile veneto, nel quale si vede MCCLX figure, quali sono tutte pronte al servitio con la sua obbedienza, & corrispondenza, che parlano l’una all’altra. This edition begins with a different dedication, dated June 24, 1616 and addressed to Venetian Doge (chief magistrate), Giovanni Bembo (1543-1618). In this new dedication Andrea Ghisi stresses the sophisticated structure of the book, which does not indulge in hazard, because in its pages “everything comes from intelligence”; the same argument can be used to describe Doge’s warfare, whose success is due more to the military value than to fate.

Left: London 1610 edition (after digital restoration) – Right: Venice 1616 edition (original).
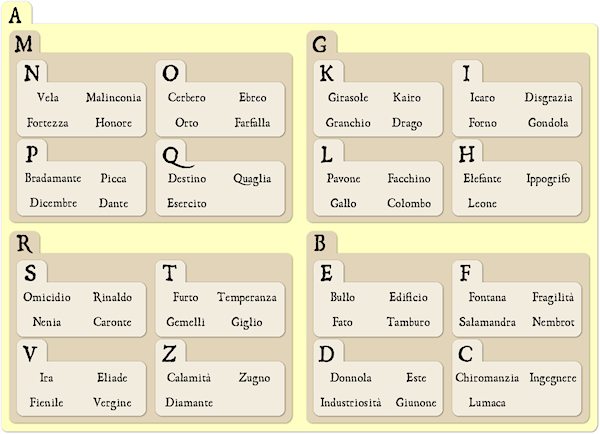
The book can be used to divine, through three questions, which figure a person thinking of, and it is composed of 21 tables, one for each letter of the Italian alphabet, each spread over two pages. Every table shows the same 60 figures, mixed in different ways and subdivided in four groups each containing 15 images.

Table A from London 1610 edition (after digital restoration).
The three editions show different figures, but they all share the principle on which the trick is based.
The analysis here is based on the English edition by Thomas Purfoot, expanded from the original, published in 1610.
Not much biographical information about Andrea Ghisi is available. The title of his most famous book presents him as a Venetian nobleman.
In an article by Carlo De Franceschi (1809-1893) there is a reference to a person named Andrea Ghisi:
Andrea Ghisi, later appointed (July 23, 1617 – September 22, 1618) mayor of [Pirano d’Istria]. (1)
Ghisi’s name is also associated with the city of Pirano d’Istria in a note from a register dated December 22, 1617:
Given the serious damages caused to Andrea Ghisi – destined to become the mayor of Piran – the Uskoks and citizens of Trieste who partly plundered and threw into water his furniture, which was on its way to that city, are fined one thousand ducats. (2)
Since 1283 the town of Piran had been under Venetian control, which is coherent with the dedication to the Doge of Venice in 1616. In the absence of other elements, however, we cannot exclude a simple case of homonymity.
In 1633 Estêvão Rodrigues de Castro, a poet in the service of “Duke of Ghisa”, titled one of his sonnets “Soneto sopra quella impresa del Laberinto col moto In silentio et spe”. Here are some verses:
Vive il cor mio tra silenzio et speme […]
forte, intrepido, audace et non mai vinto,
in mezzo del horror d’un laberinto
brama assai, troppo spera et nulla teme.
My heart lives between silence and hope […]
strong, fearless, bold and never beaten,
in the middle of a horrific labyrinth
desires a lot, hopes too much and is not afraid of anything.
Although the reference is to a vague “labyrinth”, the Portuguese scholar Giacinto Manuppella considers very likely that the source of the poet was the book by Andrea Ghisi. (3)
In the eighteenth century, the book is listed in the catalogues of several libraries, including that of Victor-Marie d’Estrées (1660-1737) (4) , Philipp von Stosch (1691-1757) (5) , Gottfried Thomasius (1660-1746) (6) and Louis César de La Baume Le Blanc (1708-1780) (7) .
In 1753 a pseudonymous author, Jonathan Puzzle, published The Labyrinth: being an exercise for wit and humour by rational rebusses (printed by James Hoey, Dublin) (8) . The title of this book plays on that of the 1610 English edition of Ghisi’s work. It presents a series of 140 word games involving the use of verbal rebus riddles, by which the clues are made up of words as syllables, combined to produce a final word as a solution.
In 1831 Andrea Ghisi’s game is described briefly by Count Leopoldo Cicognara in his Memorie spettanti alla storia della calcografia (9) , without any reference to the trick on which the book is based.
In 1857, the French scholar Paul Lacroix (1806-1884) published an article dedicated to playing cards (10) , citing the English edition of Laberinto and saying that some of its 60 images come from the Mantegna Tarot, with the exception of 5 figures which have been replaced for alphabetical reasons. In the same period, Andrea Ghisi’s book and its relationship with Italian Tarots are at the core of a curious controversy between Lacroix and a Parisian scholar, Romain Merlin (1793-1876), about the origin of playing cards. (11)
In 1911 Robert M. Burch and William Gamble cite the 1616 edition of the book, not for its content, but for a peculiar physical characteristic: its woodcuts are all in red colour. (12)

Close up of a table from Venice 1616 edition.
In 1946 the English edition of the book is quoted in an article by Frank Percy Wilson (1889-1963) about Dante Alighieri’s portraits in English literature. Wilson’s interest is focused on Dante’s silhouette that appears between the 60 pictures in the book. In a paragraph entitled “Wits Laberynth (1610)” the scholar briefly describes the game, without going into details of the structure on which it is based,
...which it would be tedious and impertinent to relate. (13)
In an article about sixteenth-century engravings, Jochen Becker uses the Dutch adjective “willekeurig” (random) to describe the arrangment of the images in Laberinto. At the same time, the scholar admits that the game offers no freedom to the player; the path through the tables is guided and unique:
It is a game that does not allow any control, whose players can act only as a puppet. (14)
In a recent academic talk (15) , the Egyptian scholar Nadya Chishty-Mujahid categorically denies the esoteric value of the work, but also its connection with playing cards:
I must clarify that in essence, Laberinto appears to have absolutely nothing to do with either divination, with which the Tarot has gradually become associated over the years, or even with basic card-play.
At the same time, the scholar is pessimistic about the possibility of finding an order behind the grid of images offered by Andrea Ghisi:
However, in spite of all the effort that obviously went into the creation of Laberinto, the deep and perhaps exciting mystery that this pictorial maze presents is unfortunately tinged with the frustration that arises from the complete absence of any fixed or set rules by means of which this game might be played.
In 2006, in an article dedicated to book tests (16) , Max Maven credits Vanni Bossi as the one who introduced Andrea Ghisi’s book to the magical community. Questioned on the subject, Bossi writes on May 28, 2008:
I worked for several years on Ghisi’s Laberinto, which this year will be published in facsimile accompanied by an essay, more or less in the style of the already published works on Galasso and Cardano. A lengthy commentary on it is also present in my study of Italian magic that was almost ready for publication at the end of 1999, when I had to stop because of my wife’s illness and subsequent death. I only recently started to work on this project with new additions. I think it will be ready for publication next year. (17)
Unfortunately Vanni Bossi died in December 2008, taking with him his research into the secrets of Laberinto.
It is not easy to take the baton to complete Vanni’s work: the notes he left behind are bulky and can not be accessed quickly; the heirs are meticulously sorting them, but the notes on the book by Andrea Ghisi have not been found yet.
If I want to rebuild Laberinto I have to start the work from the beginning, but I have to face a series of obstacles. Vanni Bossi was able to work on a Xerox copy of the English edition, inaccessible to me. I feel like William of Baskerville, who in The Name of the Rose is forced to reconstruct the structure of a labyrinthine library, without being able to enter it.
On October 14, 2009 Michael J. Hurst provided a good theoretical description of Laberinto in a web forum dedicated to Tarots and their history:
It’s a trivial parlor trick, a 3-step guessing game. [...] The method for determining which figure was selected took three steps. In the first step, the person identified which of four groups, the four groups of 15, his subject was in. This instantly eliminated 3/4 of the possibilities. (If there had been only 4 subjects, this would have been the end the selection process.) Each of the four groups leads to one of four secondary pages, where the person again identified which of the four groups on that page his subject was in. This is where the arrangement becomes important – because of the arrangement of the pictures on the secondary pages, this eliminated 3/4 of the remaining possibilities. The arrangements were meaningless but crucial, sub-dividing the initial groups so the selection process conveyed far more information than it seems. (If there had been only 16 subjects, this second selection would have ended the elimination process and identified the subject.) This same process takes place a third time. (If there are only 64 subjects – and there were in fact only 60 – this ends the selection process.) The selected array on this third turn is the answer array.
The idea of identifying an object through a series of questions can be found in a 1478 manuscript by Luca Pacioli, where the method is used with 16 stones. (18) Hurst clearly describes the core principle of the game, allowing the creation ex novo of a book like Laberinto, but since it does not offer a specific and complete map of the book, it cannot be used to create a facsimile.
In May 2010 I met Bill Kalush, founder of the Conjuring Arts Research Center, who told me that a PDF version of the 1610 edition is available in the database of Ask Alexander.
Some months later, Herzog August Bibliothek published on its website a PDF version of the 1616 edition. The material is enough for a complete analysis of Laberinto.
The creation of the facsimile is made up of several stages. Each figure was first scanned and digitally restored to remove dirt and distortions due to the poor condition of the pages. With 1260 woodcuts arranged, following the same structure as the original book, the risk of making an error is very high. So, I involve my computer by making it “walk” through all 60 possible paths, starting from each figure. The “electronic check” locates all my errors and allows me to correct them. The most difficult stage of the work is the recognition of all the 240 small numbers appearing on four tables. Many of them cannot be read, and I feel like I am playing a giant game of Sudoku: at first I have to discover the logic used to assign each number to the figures, the relationship between numbers in different tables and finally prepare a second “electronic check” to verify the correct working of all the possible choices. The holes are progressively filled, and after some hours the grid is complete. Following the transcription of the numbers next to the 240 figures, I proceed to a second check to rule out any errors. I decide to correct two inaccuracies in the original text, already reported in the 1610 edition of the book: the transposition of the last two images in table Z and the wrong transcription of two numbers in table M.
When the facsimile is ready, I can start to map its structure: Laberinto shows a fascinating layout, chaotic and redundant for almost 70% of its images; the islands of order are few but crucial. As a protoexample of hypertext, here is how to use it to read minds.
Ask someone to choose one of the 60 images displayed in table A and to tell you in which group it appears:

Look at the first image of the group chosen: the first letter of its name will tell you which is the next table. If Tamburo (Drum) is chosen, you’ll be told that the image is in the group IV, whose first figure is the Bullo (Fencer):

Open the book at table B (the first letter of the word Bullo), and ask to find the original image and tell you in which group it appears:

As before, the first letter of the first image of the indicated group will tell you which is the next table. In the previous example, Tamburo is in group I, which begins with the Edificio (Architect).
Open the book at table E and ask for the group in which the chosen image can be found last:

In the example you will be directed to group IV. Look at the first figure in the indicated group: it starts with letter D (Dante). Starting from the first image, spell silently the letter A, then move on the second spelling B, going on until you reach D: the figure you are on is the one which has been thought.
Keep in mind that the alphabet to be used is the Italian one: A, B, C, D, E, F, G, H, I, K, L, M, N, O, P, Q, R, S, T, V, Z. (19)
The book owes its title to the path you need to follow through its tables, which should not be read one after another in a sequential manner: each page can lead to different tables, each time offering four bifurcations, and it is the choice of the initial figure which determines the route to take, through what appears to be a complicated maze. Observed on the surface, the structure of the book by Andrea Ghisi is so chaotic that it seems to defy any attempt to draw a map. The 1260 images (that wrongly become 2260 in the title of 1607 and 1610 editions) appear to be randomly arranged but some believe that their order hides a deep esoteric symbolism, known only to initiates. Adam McLean, for example, confesses his inability to reveal the mechanisms of the book, suspecting the presence of a hermetic message hidden between its winding paths:
Whether this work has any hermetic import I am unable to say, as I have not been able to solve its enigmatic structure. The use of the Tarocchi of Mantegna derived emblems may have little significance, since the first edition used another set of images. However, the fact that the work was published in this form in 1616, during the explosion of hermetic and alchemical publications, is very suggestive that some hermetic riddle is woven into its strange structure.
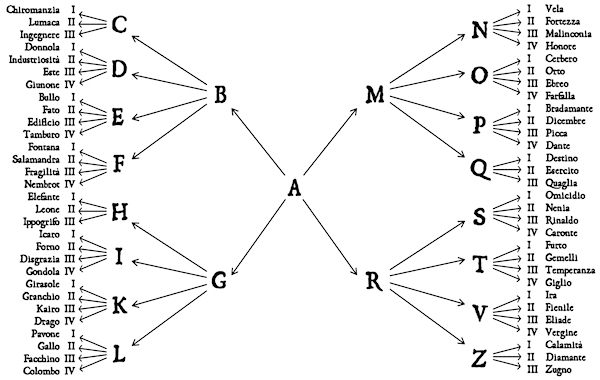
In fact, the structure that unfolds through the 1260 images can be reconstructed with relative ease, based on the assumption that each of the 60 figures is reached through a single path: analysing all of them, it is possible to discover the method used by Ghisi to shape its labyrinth. Since three tables are enough to divine any image, each path can be described with the 3 letters identifying them. In order to divine Tamburo we started from table A, we moved to table B and finally to table E, where the figure appeared in the group IV; therefore the path leading to Tamburo can be identified by the sequence ABE4.
Since the game starts from table A, all paths will start with the letter A. And since the four groups of table A start with Bullo, Girasole, Malinconia and Rinaldo, the second letter of each path will be one of the following: B, G, M, R.
By analysing separately tables B, G, M and R we can identify an interesting rule: the peculiar arrangement of the images prevents any path from returning to a previously visited table. On the contrary, all paths lead to a table in a following position in the alphabet. Therefore the 21 tables can be divided in three groups, according to the position occupied in the 60 paths:
Tables in position 1: A
Tables in position 2: B,G,M,R
Tables in position 3: C,D,E,F,H,I,K,L,N,O,P,Q,S,T,V,Z
Sorting all the 60 paths into alphabetical sequence, the result shows a certain degree of order.
Each of the tables in position 2 leads to one of the four tables following in the alphabet: table B leads to tables C, D, E and F, table G leads to tables H, I, K and L, and so on.

All the paths end on one of the 16 tables in position 3, and given the fact that each table is made up of four groups, in theory we could put 16 × 4 = 64 figures; since the figures involved are only 60, there are a total of 4 groups which are not at the end of a path. Andrea Ghisi chose to distribute the 4 empty groups with an admirable sense of symmetry, choosing the fourth group of tables C, H, Q and Z.
To better appreciate the hidden order behind Laberinto, you can find here a graphical map of its structure as a series of Chinese boxes:
As if it were a file, each table is marked with a label in the upper left corner, and is divided into four groups. Table A presents four sub-tables, each of which contains four sub-sub-tables inside. These contain the names of 4 figures. The map allows you to foresee, at a glance, the path leading to each figure: Salamandra, for example, is in group IV of table A, in group III of table B with a grey background, and finally in group II of table F. Therefore the path towards Salamandra can be expressed as ABF2. If you check it with the actual book, the map allows you to foresee all the groups and tables along the path starting from any other figure. Another way to picture a map of the paths leading to the 60 images is this:
The graph makes it easier to understand its structure.
On the graph, a Roman numeral next to each figure identifies the group in the final table. The graph makes clear the hidden symmetry of Ghisi’s work: the fourth group is missing from table C (the first from above) and from table Z (the first from below), but also from table H (the fifth from above) and from Q (the fifth from below).
Once we have identified all 60 paths, it is easy to see that the vast majority of images that appear in Laberinto are reproduced for the simple purpose of misdirection: if, as we have seen, the path that leads to Salamandra is ABF2, the Salamandra which appears in table C will never be considered during the game, because it is out of the route from table A, across table B until table F, and the same can be said of all other Salamandra that appear in tables that differ from A, B and F. The only necessary images are those that meet one or more of the following two criteria:
• they are on a table whose letter is on its corresponding path;
• they open a group in a table in position 2 or 3, except for groups IV of tables C, H, Q and Z.
In order to enliven the interactive book by Andrea Ghisi, I created a playable digital version: click here to play.

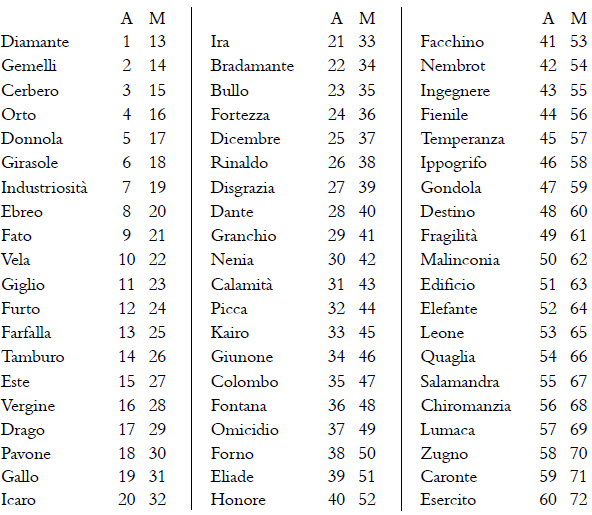
In London 1610 edition, tables A, M, S and Z show some numbers below each image: they allow you to perform a second mind reading trick and constitute the English extension of the Italian edition. Ask someone to think of a number between 1 and 60 and look for the corresponding image in table A. Browse the book to table M and invite him/her to find the same figure, bearing in mind the corresponding number, which will be different from the first. Open the book at table D and ask him to look up the number found in table M, keeping in mind the figure which corresponds to it; it will be different from the image in the table A. Finally, ask him/her to find the figure in the Z table, and tell you its number. By simply subtracting 6 from it, you’ll discover the number initially thought of.
Citing the example provided by Andrea Ghisi himself, suppose that number 40 is thought of. It appears under Honore. The same figure in table M corresponds to number 52. Look up the number in table S and you will find it under Fortezza. The same image corresponds, in table Z, to number 46. By subtracting 6, you get 40, the number thought of.
The route to guess the number is deliberately convoluted in order to confuse the player, but we can unravel it to recognize three simple steps. In table A, the numbers from 1 to 60 are listed, each corresponding to a different figure. In table M each figure shows a higher number of 12 units compared to table A. So Diamante, bearing number 1 in table A, in table M corresponds to number 13 (= 1 + 12). This applies to all figures, up to Esercito, which corresponds to 60 in table A and 72 in table M. Therefore table M shows all numbers from 13 to 72.
Once a number N is thought of, finding its corresponding image in table M is the same as performing the operation N + 12.
If someone thinks of the number 1, at first he see that it corresponds to Diamante, then he looks up the same image in table M and here the new number below Diamante is 13.
Here is the list of the numbers corresponding to each image in tables A and M:
Moving from table M to the following table is just misdirection: also table S shows numbers from 13 to 72, but the corresponding images are all mixed up. The person involved in the game should limit himself/herself to looking up the new figure corresponding to the number found in table M, and the same image should be found in table Z. In this latter table, each figure has a lower number of 6 units compared to table S.
In summary, moving from table A to table M the number N becomes N +12. In the transition from table M to table S, only the figure of reference changes, but not the number. In the final step from the table S to the table Z, the number is reduced by 6 units, making it N + 6. At this point, it is sufficient to subtract 6 to go back to the initial number. Here is the list of numbers corresponding to each figure on the tables S and Z:
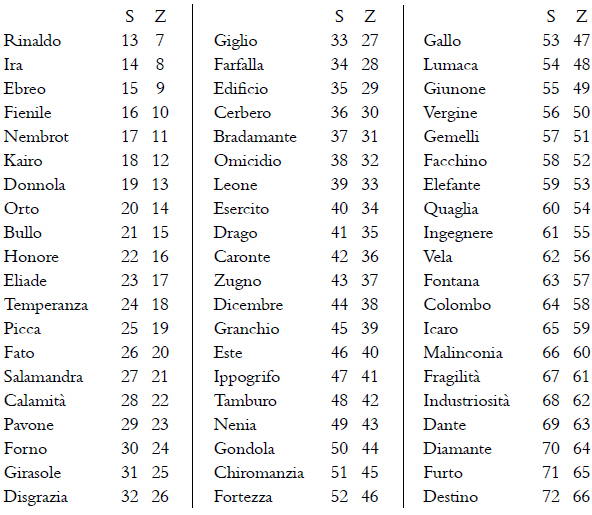
Coming back to the example of Diamante, in table M we have found the number 13. In table S, it corresponds to Rinaldo, which in table Z is assigned the number 7. Substracting 6 from it, we get 1, which is the number thought of.
Therefore the complete path from the number thought of to the one in the table Z is forced:
Table A – Number N is converted to figure AN.
Table M – Figure AN is converted to number N+12.
Table S – Number N+12 is converted to figure SN+12.
Table Z – Figure SN+12 is converted to number N+6.
Here are the 60 numerical paths through the four tables in Laberinto:
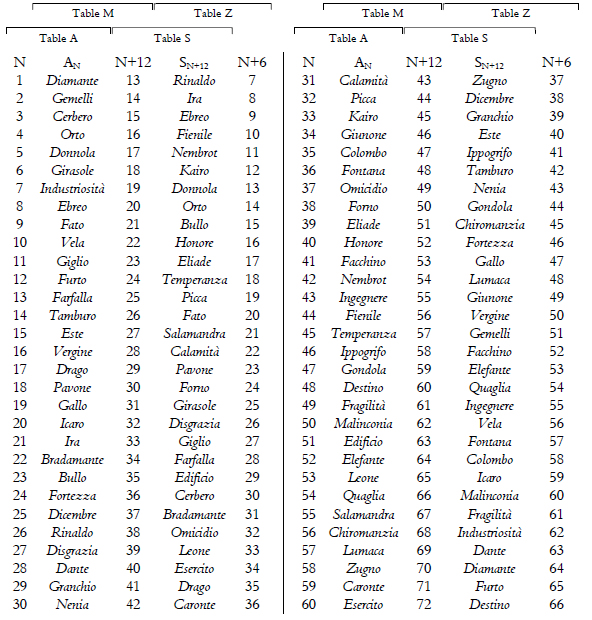
In order to read the table properly, let us consider the last row. If we think of the number 60, this can be found below Esercito in table A. In table M Esercito corresponds to number 72, which in table S is below Destino. This image bears the number 66 in table Z, and by subtracting 6 we are back to the number we thought of.
In 1613 viscount Francesco Gattici published La Zecca Aritmetica con mirabile secreto at the Venetian typographer Giacomo Sarzina (20) . This book shares the same structure of Laberinto, with some interesting differences. Printing Gattici’s book was cheaper because there is no figure on it: its 1260 squares show only three distinct series of words. Using the book, the player may choose between three different divinations: the currency of a coin, the name of its owner or the city he lives in. Every square contains the name of currency, the last name of a person and the name of a city.

As in Laberinto, each page was divided into 4 squares, which were assigned names: if you played with the cities, each square corresponded to a European population dominating the cities (Italian, French, Spanish and German), if you played with currencies, the four squares corresponded to four different bankers owning the money, if you played with last names of person, the squares corresponded to four continents (Asia, Africa, Europe and New World), indicating the whereabouts of the person concerned. So, if you played with the city and someone thought of Ravenna, the question to ask was not “In which square is the city you’re thinking of?” but “What people are dominating the city you’re thinking of?”. On Table 12, for example, Ravenna was in the square labeled as “Italians”, so you could answer: “It is under the domination of Italians.” If you play with people’s names, the table 12 would have said that Peter was in Africa, instead of saying that he was on the fourth square.
The attempt to make “significant” the question to ask, compared to that of the original Laberinto, testifies a sophisticated illusionistic thought by those who had reworked the idea of Andrea Ghisi. In addition, the introduction of three distinct lines of play in the same book is a significant expansion compared to the 1607 edition of Ghisi.
By contrast, La Zecca Aritmetica was less subtle in misdirecting the arithmetic method to jumping from one table to another: while Laberinto was based on the first letter of the first figure of each panel, each element in La Zecca was labeled with a number whose role was incomprehensible to the player, and the first number on the square indicated the next table. Since the presence of these numbers was not justified in any way, the mechanism of transition from one table to another was less elegant.
Special thanks to Marcus Williamson for the help in translating this post. Thanks also to Ferdinando Buscema, Nadya Chishty-Mujahid, Michael J. Hurst, Bill Kalush, P.G. Varola and Francesco Arlati for the kind support and the material provided.
1. Carlo de Franceschi, “Il ramo istriano della famiglia Bembo” in Atti e memorie della Società istriana di archeologia e storia patria, Volume 61, 1961, pages 99-122.
2. “Senato Mare. Cose dell’Istria”, trascrizione del registro 75 in Atti e memorie della Società istriana di archeologia e storia patria, Volume 12, 1897, page 441.
3. Giacinto Manuppella (ed.), Estevao Rodrigues de Castro. Obras Poéticas em portugues, castelhano, latim, italiano, Por Ordem da Universidade, Coimbra, 1967, page 598.
4. Catalogue des livres de la bibliothèque de feu monseigneur le maréchal duc d’Estrées, Volume 1, Jacques Guerin, Paris 1740, page 278.
5. Bibliotheca Stoschiana sive Catalogus selectissimorum librorum quos collegerat Philippus liber baro de Stosch, Florence 1759, page 213.
6. Bibliothecae Thomasianae sive locupletissimi thesauri ex omni scientia librorum praestantissimorum rarissimorumque quos olim possedit vir illustris Gottofredus Thomasius, Volume 3, W. Schwarzkopf, Nürnberg 1769, page 172.
7. Catalogue des livres de la bibliothèque de feu M. le Duc de la Vallière, Volume 2, Nyon, Paris 1784, page 495.
8. Jonathan Puzzle, The Labyrinth: being an exercise for wit and humour by rational rebusses, James Hoey, Dublin 1753. (Thanks to Marcus Williamson)
9. Leopoldo Cicognara, Memorie spettanti alla storia della calcografia, 1831, page 172.
10. P. L. Jacob [Paul Lacroix], Revue universelle des arts, Volume 5, page 104.
11. Romain Merlin, Origine des cartes à jouer, Rapilly, Paris 1869, page 46.
12. Robert M. Burch & William Gamble, Colour printing and colour printers, Baker and Taylor, 1911, page 42.
13. Frank Percy Wilson, “A Supplement to Toynbee’s Dante in English Literature” in Italian studies, Society for Italian Studies, Volume 3, 1946, pages 50-64.
14. Jochen Becker, “Plaatjes en praatjes: emblemata, gespreksspelen, conversatie en kunstgeklets” in De zeventiende eeuw, Volume 15, Verloren, Hilversum 1999, pages 118-130.
15. Nadya Chishty-Mujahid, “An Examination of Andrea Ghisi’s Venetian Labyrinth Game and its Hermetic Predecessor, the Mantegna tarocchi”, Renaissance Society of America Annual Meeting, Venice (April 9, 2010).
16. Max Maven, “Book Tests – The History”, Magicseen, number 11, November 2006.
17. Private communication with author.
18. Codice Vaticano Latino 3129, pages 220r and 220v (now in Dario Bressanini & Silvia Toniato, I giochi matematici di Fra’ Luca Pacioli, Edizioni Dedalo, Bari 2011, pages 60-68). The trick is also described in chapter 69 of De Viribus Quantitatis (now in Luca Pacioli, De Viribus Quantitatis, transcription by Maria Garlaschi Peirani from code n. 250 in Biblioteca Universitaria di Bologna, Ente Raccolta Vinciana, Milan 1997, pages 161-162). The principle appears also in the collection by Claude Gaspar Bachet, Problemes plaisans, qui se font par nombres, Pierre Rigaud, Lyon 1624 (1st ed. 1612), pages 152-154 (problem XIX).
19. Modern Italian language does not include K and includes U between T and V.
20. Francesco Gattici (Massimo Rizzardini ed.), La Zecca aritmetica, Lupetti, Milano 2008.
BY-NC-SA 4.0 • Attribution-NonCommercial-ShareAlike 4.0 International