MARIANO TOMATISWONDER INJECTORItalian writer and magician
|
 Stop bombing GazaPosted on saturday 26 july 2014, 13 days before scifoo14 • Written by Mariano TomatisBertrand Russell wrote that «The world is full of magical things patiently waiting for our wits to grow sharper.» By using the expression “growing sharper”, what was he referring to? Our wits, probably. But I opt for a better interpretation: maybe he was saying that our wits could make magical things sharper. This is a short film by me about the concept of “sharpened magic” (embedded English subtitles available): Relegating magic to a childish form of entertainment is a way to avoid to confront its sharper implications. Because magic is a martial art using wonder to wake up from sleepwalking and force us to open our eyes. Magic & Re-enchantmentPosted on wednesday 23 july 2014, 16 days before scifoo14 • Written by Mariano TomatisWhen I was a child, every half hour I ran to the hen-house to check if the chicken had laid an egg. Incredible as it may sound, every time I found one. Brimming with enthusiasm, I brought it to my uncle. Half an hour later the scene was repeated — and so it went, for all day long. Only a few years later, when my uncle passed away, I was able to explain such fertility. Thanks to a confession from his wife, I found out that he was the one secretly reloading the basket, to renew my sighs of amazement more frequency than Mother Nature would have allowed. Although he didn’t look like David Copperfield — nor he attended Hogwarts (he even left school at third grade) — it’s hard for me not to consider him the greatest magician of my childhood. But were he still alive, and reading this, he would react with skeptical frown. And understandably so. Till yesterday, the Magician have been a very special individual: a Superman endowed with irresistible powers, allowing him to rise above the common herd. Sawing and restoring women cut in halves, he shows how to dominate life and death. Breaking free from any constraint, he challenges the gods, just like Prometheus did. Subjugating people with his hypnotic fascination, he is a valuable resource in a marketing-driven capitalism. No, this is not my uncle’s portrait. His magic was more intimate and humble. A discipline whose essence Samuel Sharpe caught writing: The underlying purpose of magic […] is not to deceive people but to encourage them to approach life and cosmos in a state of wonder. (1) What if it was now time to redefine the very concept of Magic? Breaking down the walls of theaters and allowing Magic to invade the world? How about giving Magic back to the common people, to encourage new stories and new wonders?  Homage to Giuseppe Pellizza da Volpedo’s “The Fourth Estate”. This is the spirit with which me and Ferdinando Buscema wrote Amaze: the first magic book open to anyone. You don’t need a stage (or a pedestal) to re-enchant the world. On the contrary, one must dirty his shoes with the mud of a chicken coop. Doing it is not that difficult. Start realizing that the world does not work properly and be willing to fix it. If the most precious vocation of magic is to “hack reality”, to become everyday magicians is not only possible: it is necessary. The existence of a mainstream kind of Magic, that makes its own navel his horizon, should not stop you. The dominant story that comes from the stages can be opposed with many other narratives from the bottom of the pyramid. Because, as Wu Ming have been relentlessly repeating, The only alternative to put up with a story, is to tell thousands different stories. _________________ (1) Samuel Henry Sharpe, Art and Magic, The Miracle Factory, Los Angeles (CA) 2003, p. 183. Magic & Bay AreaFrom Turin to Bay Area for the funniest Mesmeric Act ever Posted on tuesday 22 july 2014, 17 days before scifoo14 • Written by Mariano TomatisThere is a curious connection between the city I live in (Turin, Italy) and the Bay Area. Italy’s first capital city in 1861 and home to the House of Savoy (the royal family), Turin has always been open to esoterists, alchemists, astrologers and clairvoyants. At the end of 18th century it hosted the first Mesmeric Society founded by Sebastiano Giraud. In 1939 Giorgio de Chirico, founding father of Metaphysical Art, defined Turin the most deep, enigmatic, and disquieting city, not just in Italy but in the whole world. According to a local tradition, Turin lays on the vertex of a giant “Black Magic Triangle” together with London, England and San Francisco, CA.  As a homage to this impalpable liaison, I have just submitted the abstract for a “Lightning Talk” to be given at Sci Foo 2014: “A truly Mesmeric Act”. My Lightning Talk at Sci Foo 2014: a truly Mesmeric Act Far from the obscure implications of Black Magic and VooDoo practices, my talk will be a 5-minute playful experience involving all the audience at once: a magic act lying at the intersection between recreational mathematics and the tradition of Italian historical novels. Its recipe? Just mix a brain teaser by Martin Gardner, the atmosphere of a baroque building in Turin and an unexpected, subversive ending in San Francisco sauce. Will you attend the shortest and funniest Mesmeric Act you will ever experience?  Magic & OrigamiHow to create two linking rings out of a newspaper Posted on monday 21 july 2014, 18 days before scifoo14 • Written by Mariano TomatisIn the 19th century the Italian painter Giacomo Mantegazza (1853-1920) depicted a woman performing the linking rings magic trick.  Would you like to get two linking rings out of a piece of paper? My videotutorial will teach you how to get two linking rings out of a single page of a newspaper. ...or not? Magic & TeachingA Mathemagical Lab for educators Posted on tuesday 8 july 2014, 31 days before scifoo14 • Written by Mariano TomatisMagic can be used in school to stimulate students’ curiosity. Are you a math (or computer science) educator willing to involve your students in a magic trick with educational purposes? With the material here provided you will entertain your students for a few hours with a non-trivial mathematical analysis, kicking off with a magic trick. Each student needs these 7 playing cards:  They can easily create them with a crayon and some pieces of paper. Premise Since the 19th century, mathematics has supported criminology to capture criminals. The French Ravachol (1859-1892) has been one of the most famous bandits caught with a mathematical model, invented by Alphonse Bertillon (1853-1914). The bomber became so famous that even today, in France, the verb “to ravachol” means “to blow up”. Is it theoretically possible to locate a mathematical scheme in seemingly random movements of a terrorist? Please take part to this story putting your cards in front of you and following the instructions provided. You will be amazed! Reaction The repeated shuffles leads us to think that the “Black Knight” is totally lost in the deck. The pleasure springs out when the video is able to guess where Ravachol is. The absence of a magician in flesh and bones excludes the possibility of sleight of hand and leaves us puzzled. Nothing encourages a deeper analysis during the story, we are not told in advance what to expect, so we are left without a rational explanation about what happened. The wonder lasts only a moment. Quickly our brain regains control of the situation — but a certain intellectual effort is needed to put what happened in the correct, rational perspective. In that special moment, we are spontaneously triggered to start a deeper analysis of the topic. When the students are involved, wonder has lit a spark, and even without explicitly invite them to do so, they have already started to meditate upon what may be behind the curtain. For many, the urge to “fix” the cognitive dissonance arises from the discomfort of being deceived, and the impulse to prove — to themselves and to others — that are not naive. Best magicians are well aware of this dynamic, and they work against such an interpretation, shaping narratives which exclude the idea of a challenge to the intelligence of the spectator. In contrast, a teacher can direct the same energy towards the exploration of very interesting mathematical mechanisms. Observation, Hypothesis and Experiment This magic trick forces the student to follow spontaneously the different stages characterizing the Scientific Method. The Observation (of the mysterious phenomenon) is followed by the formulation of a Hypothesis. You can invite students to suggest some possible explanations, and in all likelihood one of the first hypotheses will be the correct one: the special cards stays 5th position, regardless of the number of shuffles made. The formulation of the hypothesis can be followed by the actual Experiment. Students can test the hypothesis with cards in their hands, discovering that indeed the position of the special card is invariant with respect to the repeated suffles; such verification is easier when the special card is face up in the face down deck. A few tests will be enough to confirm the hypothesis (and some students may also sense that this counterintuitive knowledge will enable them to amaze their friends with 7 ungaffed playing cards.) The study of a function After their meeting with the abstract concept of “invariance”, it is time to suggest the students some ways to go deeper in the exploration. You can do this with a question: “Is the 5th card the only one that never changes position?” The answer is far from obvious, and to verify it demands some investigation. A “brute force” approach is to shuffle the deck keeping an eye on the 1st card, checking if it does change position. Given that the cards “moves” from its position, the shuffle can be repeated keeping an eye on the 2nd card and so on — until having explored all the 7 cards. When the answer is found, you can invite them to represent graphically the results of their investigation. This step is crucial, because a graph summarizes — in a single glance — all the information gathered during the analysis. You can invite your students to use a grid like this: 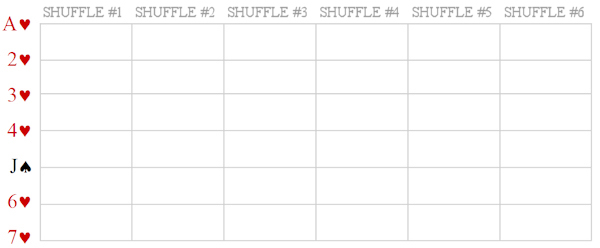 Each line corresponds to the position of a card in the DECK. The vertical divisions correspond to the shuffles. In order to keep track of the 1♥ through the deck, the students must start from the top in the upper left. The 1st shuffle moves the card from the first to the last position, so they draw a sloping red line to the bottom line, at the intersection with the vertical line separating the first two shuffles. A 2nd distribution will move the 1♥ from last to 4th position, and then the red line should be traced to the right going up to the 4th line. Proceeding in this way, the card will return to the first position after the 6th distribution. Here is the resulting graph: 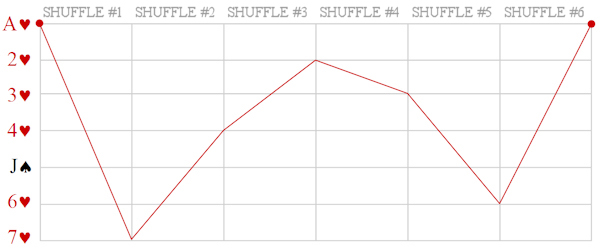 You can point out that the graph is complete, and covers the entire history of the card, even for a larger number of mixtures: since the card returns to the first position, the graph drawn by the students is cyclical; if the 1♥ is in 4th position after 2 shuffles, it will be in the same position after 2 + 6 = 8 suffles, 2 + 6 + 6 = 14 suffles and so on. The “frequency” of the route through the deck is equal to 6. The graph can be plotted for each card — and of course the most interesting is the one of the J♠ which is completely flat:  Superimposing the graphs, the “singularity” of the J♠ (and its invariant position) is immediately clear and doesn’t need any additional explanation: 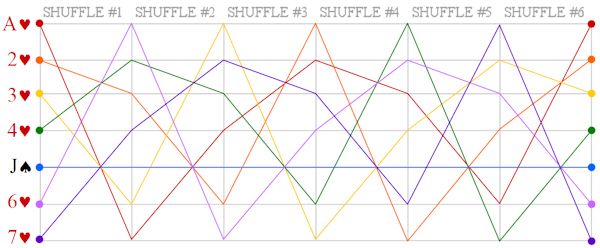 Another interesting point is that the route taken by the six “moving” cards is the same: if a card is in the first position, after the next shuffle will end up in last place, regardless of how many shuffles have been made so far; the different routes are simply shifted one to another. After drawing the graphs, the students should grasp the fact that the shuffle is nothing more than a function operating on the positions of each card, commuting them in a predictable way. Mathematically, the function is applied to a vector of seven elements and returns a vector with the same elements scrambled.  Intuitively, it may be represented by a series of tubes with seven balls: with the exception of the fifth one, passing through the tubes the balls change their relative positions. 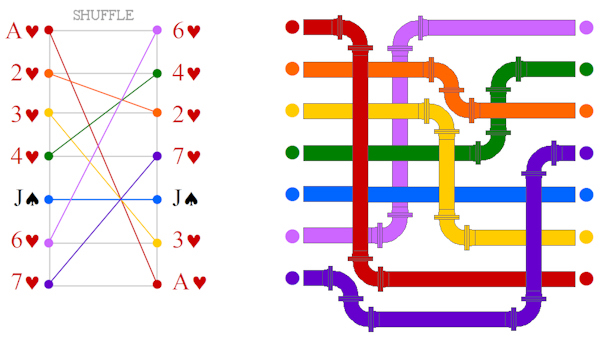 To study the effect of two shuffles is to apply twice the function to the starting vector — or more easily, to put two series of identical tubes and see the effect on the balls through them:  The cyclical nature of the function is highlighted by applying it six times, getting the starting vector as a result.  Combining six tube-structures, we would build this unlikely (and totally useless) machinery, keeping all the balls in the same order! 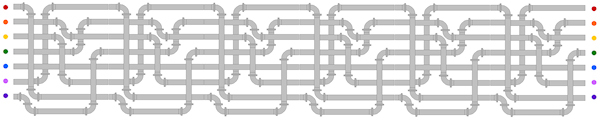 At this point the students should be particularly amazed by the idea of studying a function using a deck of playing cards. Further questions In order to show them the width of the mathematical universe that has opened up before their eyes, some interesting questions may suggest new creative ideas: • What if, after the distribution of the two groups of card on the table, you put the smaller over the bigger? Is there a fixed card also with this new distribution? What is its graph? Which is the lenght of its cycle? • What if the deck is composed of an odd number of cards other than 7? In this case, we must distinguish between the shuffle completed by putting the smaller group over the larger, and the one in which the larger is placed on the smaller. • Even more difficult: what if the deck is composed of an even number of cards? A fascinating side of the mathematical area addressed here is the existence of a large number of open questions; it is a point to emphasize, because it enables the students to live the experience of being pioneers in an unexplored region. • A bunch of 3 cards has no invariant card, but a bunch of 5 or 7 card does have it. Is there a rule for predicting whether a deck consisting of 2N+1 cards has (or not) an invariant card? • How can the shuffle be modified so that a deck of 3 cards present an invariant? How can you do the same with a generic deck of 2N+1 cards? • A deck of 5 cards has a 4-shuffles cycle; a 7 card has a 6-shuffles cycle. Is there a rule to calculate the length of the cycle of a deck of 2N+1 cards? • How can you change the shuffle so that there is more than an invariant card? The study of these questions will lead, spontaneously, to address deeper issues and to the construction of a broader theory of vectorial functions applied to playing cards. A future Science Foo CampFrederik Pohl’s Camp in a Starship Posted on monday 7 july 2014, 32 days before scifoo14 • Written by Mariano Tomatis In his short story The Gold at Starbow’s End (1972) Frederik Pohl describes a future “Science Foo Camp” hosted in a starship on a ten-year journey to Alpha Centauri. The rationale for organizing such a gathering is the desire to advance fundamental knowledge, backed by the theory that if you isolate a group of people working in diverse areas of science and technology, they will be forced to make new discoveries in fundamental sciences — especially if such thought process is not aimed at making specific discoveries. But participants are not informed about this: they think their purpose is to land on a planet called Alpha-Aleph orbiting Alpha Centauri. More damningly, a small circle of advisors know the truth about this one-way suicide mission, being aware that Alpha-Aleph does not exist! Taught basic elements of mathematics and invited to enjoy the long voyage solving recreational puzzles, the participants start to develop an efficient way of coding up messages and use it to send back messages like 1973354 + 331852 + 172008 + 547 + 39606 + 288 minus 78. The scientists on Earth face conclude that in a while the communication with Campers will become impossible for the increasing gap between their intelligence and the complexity of the issues discussed in the starship. The story has a surprising evolution that I will spoil in this Godelized form — understandable only by the travellers to Alpha-Aleph: 23747 + 101279 minus 4643 Magic & IngenuityThe Final Secret of the Illuminati Posted on saturday 5 july 2014, 34 days before scifoo14 • Written by Mariano TomatisBoing Boing is a “directory of wonderful things”, one of the most-read and linked-to blogs in the world. In June 2013, together with my coauthor Ferdinando Buscema, we have been invited by its editor David Pescovitz to create the opening theatrical experience for Boing Boing: Ingenuity, a 12-hour marathon involving scientists, artists, writers, designers, musicians... and a magician! Held in San Francisco on 18 August 2013, the event started with a performance by Ferdinando — being at the same time a magic show and a speech about creativity. (1) This is my artwork for the performance:  We have shaped “Lighting Ingenuity — The Final Secret Of The Illuminati” as a cyberpunk synthesis of magic and technology. Big fan of historical enigmas, I have contributed to the theatrical narrative with a surreal steampunk touch, hacking a Llullian Wheel (conceived in the 13th century and carved in wood in 2012 by Ian and David Metcalfe) and creating an app for a mobile phone controlling its (parapsychological) functions. See it in action in Ferdinando’s video: In the above performance, Ferdinando urges his audience to “write your ideas down” and explains that “books are the building blocks of ingenuity”. He demonstrates this with a magic effect literally bursting out from the pages of a Moleskine notebook. (2)  My favourite moment is the epic final scene, with Ferdinando interpreting Nikola Tesla revealing the Final Secret of the Illuminati: The idea came like a flash of lightning and in an instant the truth was revealed.  On the left, Nikola Tesla. On the right, Ferdinando Buscema. _________________ Magic & AlchemyThe 16th century computer and the book that kills Posted on friday 4 july 2014, 35 days before scifoo14 • Written by Mariano Tomatis Designing and recreating a wood-and-glass computer used in the 16th century? A funny activity with a certain amount of thrill, especially because the mathematical secret at its core could lead to death! It all started with the “Book of Soyga” (discover its story here), a 16th century treatise that included 18 leaves containing 36 tables of letters. Their structure has been shrouded in mystery for centuries, and — according to legend — revealing its secret would have brought to death in two years and a half. The alchemist and astrologer John Dee (1527-1608) invoked the archangel Uriel to solve the puzzle, but in vain. Four centuries later, the mathematician James A. Reeds defied the curse, discovering and publishing (1) in 2006 the method to compile all 36 tables of the “Book of Soyga”. How to fill in the “Book of Soyga” In order to create a page of the book, draw a square grid, consisting of 36 rows and 36 columns. From the upper left corner, write vertically a “magic word”, followed by itself upside down, then back upright, upside down, etc. until you have completed the column. Here’s how to fill it starting from ABRACADABRA: 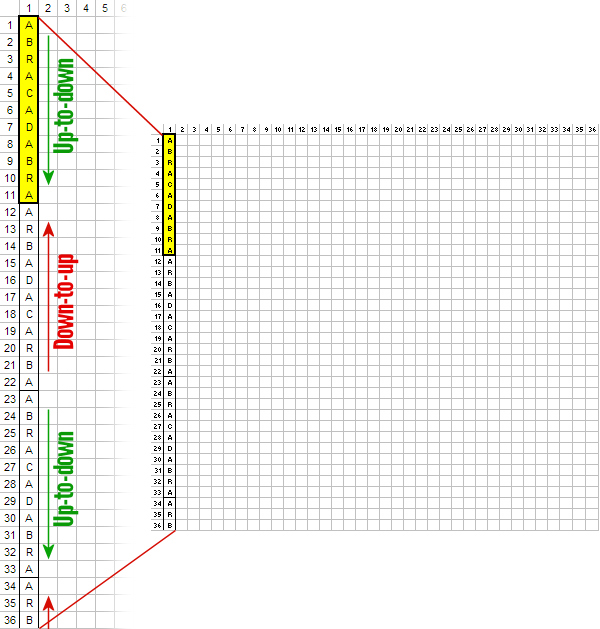 It is easy to fill in the first row. Reeds discovered that each letter is followed by another according to a simple rule: 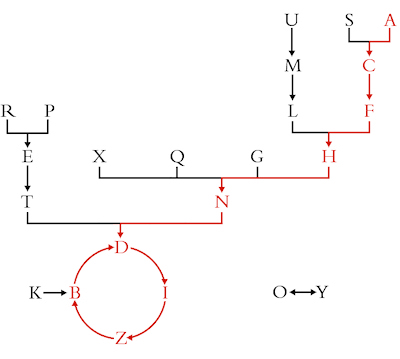 We start from the A which is in the top left square. The arrows in the diagram above show the obligatory path that leads from A to C, then to F, H, N and D, and then enters the closed circle I, Z, B and D again. Let’s write, on the first line, the path described by the rule:  Now the procedure becomes more difficult. Each of the other squares should be filled on the basis of the letter above and the one on the left, according to a mathematical rule that Reeds summarized in this equation: 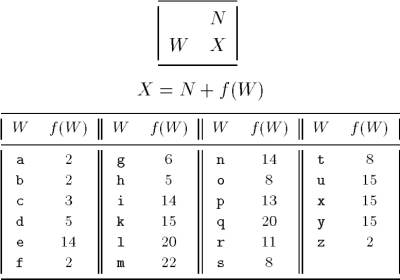 Complex enough, isn’t it? According to the equation, the unknown letter X is obtained starting from the (N)orthern letter and moving on in the alphabet a number of positions determined by the (W)estern letter. Each letter corresponds to a different shift, as indicated in the table above. (The procedure is better explained here.) Can you imagine the amount of work needed by the creator of the tables, who had to “calculate” the equation for more than 45,000 times? A modern computer can fill the table starting with ABRACADABRA in a fraction of a second (check it here), but a manual work would take months. What if they had used a computer in the 16th century? What if they had used a computer in the 16th century to compile the book? «Which kind of computer would have worked?», I asked myself. Inspired by the mnemonic wheels of Ramon Llull (1235-1316), already known at the time, and by the gift of a dear friend — David Metcalfe —, I designed a “Soyga Tables Compiler” consisting of two wheels, fixed on a wooden base:  Both wheels show in the external crown the 23 letters of the alphabet appearing on the tables of the “Book of Soyga”. The right wheel shows, at the center, arrows leading from one letter to another. A second wheel is printed on glass and fixed in the center of the first. When spun, the arrows in the background remain fixed, and being transparent, different rotations produce different connections between letters. Here is the hypothetical 16th century computer:  Such an instrument would enable anyone to compile a table of the “Book of Soyga” ignoring the complex rules described by Reeds, because it incorporates them all in a single object easy to work with. (2) In order to compile the first line, it is enough to rotate the two wheels in a way that all the letters are aligned: the arrows thus obtained reproduce the graph above and allow you to easily see the path to follow — A leading to C, then to F, etc. 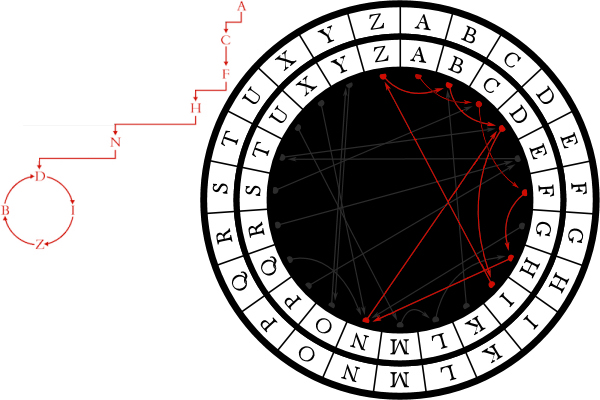 From the second row, a different rule applies, equally simple: in order to find out what to write in a square, the wheels must be rotated until the letter on the left (on the outer circle) and the letter above (in the inner ring) are aligned; now the arrow (red in the diagram) starting from the letter above leads to the letter to be written — in this case, to E: 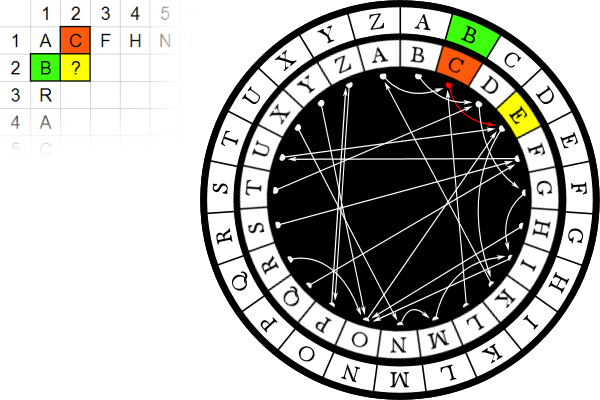 This procedure can be repeated for the entire table, square by square, and allows you to faithfully reconstruct the entire “Book of Soyga”. To better understand its use, click here: the table shown is based on the magic word ABRACADABRA, and clicking on any letter (from the second column on) you can see the interaction between the two wheels and — indicated by two red dots — the arrow that connects the letters involved in the encoding procedure:  _________________ (1) Jim Reeds, “John Dee and the Magic Tables in the Book of Soyga” in Stephen Clucas (ed.), John Dee: Interdisciplinary Studies in English Renaissance Thought, International Archives of the History of Ideas, No. 193. Dordrecht, Netherlands: Springer, 2006, pages 177-204. The article can be downloaded from here. (2) I stress again that, to date, there is no description of a computer like that, which I designed in a totally hypothetical way, limiting myself to technologies and mathematical knowledges available at the time. Magic & Secret MessagesA “Hey, but… it’s me!” experience for your friends Posted on thursday 3 july 2014, 36 days before scifoo14 • Written by Mariano TomatisOne chapter of our book L’arte di stupire (“Amaze”) is dedicated to the “Hey, but… it’s me!” experience, the short circuit you experience when you look at someone and suddenly… bam! You realize that that someone… is yourself! There’s a “hey”, expressing the encounter with something unexpected. There is a “but”, which reveals the contrast between what seems and what really is. The ellipses highlight the time it takes to do a U-turn, shifting our point of view and questioning our own perceptions. “It’s me” is the final revelation, the moment in which everything is seen in a different light. Coming full circle is what Douglas Hofstadter calls “a strange loop.” Fredric Brown’s “The Sentinel”  The science fiction writer Fredric Brown was a master designer of magical experiences in the short story format. His best-known story “The Sentinel” (1954) recounts the story of a man landing on a planet 5,000 light years from his home. Waiting for him were the other intelligent race everywhere in the galaxy… cruel, repulsive, hideous creatures, horrible monsters. He kills one, then shudders at the sight of the corpse. The story ends with the description of the horrible inhabitants of such an alien planet: They were horrible disgusting creatures, with only two legs, two arms, two eyes, that sickening white skin and without scales. And the spell is completed. The short circuit kicks in, and we realize that the story’s protagonist is an alien, and the monster… an earthling like us! The two crop circles created by Francesco Grassi In 2013 Francesco Grassi — the man who has “initiated” me to the secrets of this Magic Art — created with his team this wonderful crop circle:  Robella 2013 The work was interrupted when dawn came, the picture left incomplete and a secret message only partially encoded. In 2014 the same circlemaker created a (double) circle with a number of similarities with the one of the year before (see it on Boing Boing):  Marocchi 2014 This second crop circle also encodes a secret message, incomplete too: as explained by its creator (in this tweet), only overimposing the two pictures the enigma can be solved! 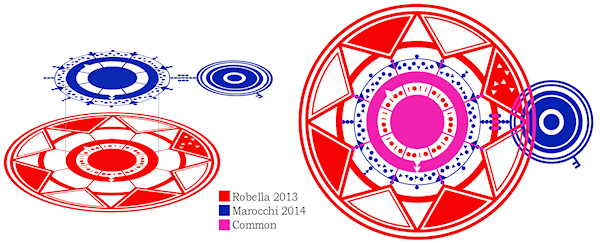 My artwork explaining the correct link between the two crop circles What is the complete message? Unfortunately I have no idea at all! Francesco Grassi hasn’t reavealed it yet, in order to let the researchers solve the intricate puzzle by themselves. This challenge has a pretty funny side. Some believers argue that “Robella 2013” was not created by humans, but to explain the correlation between the two (half) messages the incredible hypotesis is that Francesco has fixed a broken alien message with a human crop circle! This is really interesting, the way how someone can push higher and higher the boundary of cognitive dissonance. Such an attitude deserves a cruel reply, so… A “Hey, but… it’s me!” experience for your friends Would you like to discover that the two crop circles hide… your name? Now you can gift your friends with this incredible experience, clicking this link: ENCODE A NAME IN A CROP CIRCLE Write here a 8 letters name (e.g. MAX MAVEN) and you will get a customized link to share with your friend: the page will be a (fake) discussion board with a post by Goldrake revealing of having discovered the name MAXMAVEN (or any other name) in the two crop circles (see here the post about MAXMAVEN). Julian Baggini’s Mozzarella Moon The idea of a half-human and half-alien message may sound absurd, but there is someone actually believing it. It reminds me of the wonderful The Pig That Wants to Be Eaten (2005) written by the English philosopher Julian Baggini (who will attend Science Foo 2014).  One chapter is titled “Mozzarella Moon”: The moon is made of cheese-mozzarella, to be precise. […] «But men have walked on the moon,» you say. Wrong. It was all a fake, filmed in a studio by NASA. Haven’t you seen the movie Capricorn One? If it weren’t for lawyers, that would have been billed as a documentary. «But other non-manned trips have been made to the moon.» Most of them were fakes too. Some weren’t, and those were the ones that brought back samples proving the mozzarella theory. But of course the evidence has been suppressed. Baggini concludes by asking: «How else would Elvis be able to stay alive up there if he didn’t have an endless supply of cheese?» His explanation of why people tend to believe weird things is one of the shortest and effective — and applies well also to the surreal theories about crop circles: Conspiracy theories are made possible because of two limitations of knowledge formation. The first is what could be called the holistic nature of understanding: any single thing we believe is connected, web-like, to any number of other beliefs. So, for example, your belief that ice cream is fattening is connected to your belief’s about the calorific content of ice cream, the connection between fat consumption and weight-gain, the reliability of nutritional science and so on. There is overwhelming evidence that Francesco Grassi and many other circlemakers around the world have created the best crop circles out there, «but we are not compelled by the evidence to reach this conclusion.» The evidential gaps mean that the evidence can be made consistent even with the hypotesis of a man completing an alien message: All we need to do is rearrange all the other interconnected beliefs we have in our web of understanding so that they too fit. Julian Baggini concludes: For sure, what you end up with can sound pretty wild. But the crucial point is that it fits the evidence. We have to admit it, before any attempt to reassess the human skill in modelling crop fields and the great value of Occam’s Razor. Magic & AwarenessBe smark! Lucid self-delusion in Robert-Houdin’s magic Posted on friday 27 june 2014, 42 days before scifoo14 • Written by Mariano TomatisIn an article (1) dedicated to Jean-Eugène Robert-Houdin, the father of modern magic, Joshua Landy highlights the innovative aspects of his approach to conjuring. He was the first magician to abandon ceremonial robes and ritual formulas of esoteric tradition. He dressed in civilian stylish clothes, claiming the domain of science and reason on the charlatanism. His books unveiled the misdeeds of witches and cardsharpers, and his art was explicitly designed to offer new experiments divested of all charlatanism. (2) As Landy points out, he generally considered himself an active force for disenchantment, a champion of enlightenment in its continuing struggle against credulity. Nevertheless, Robert-Houdin is remembered as one of the finest (re)enchanter of his era. How could he reconcile the two attitudes? Landy illustrates the paradox by describing one of the most well-known magical effects of the French magician — the “ethereal suspension” (1847). He announced it on stage with these words: Gentlemen, I have just discovered a new, truly wondrous property of ether. When this liquid is at its highest degree of concentration, if a living being breathes it, the body of the patient becomes in a few moments as light as a balloon. After this introduction, the son of Robert-Houdin was raised in a horizontal position, supported on one side by a simple stick, demonstrating the possibility that a human being could levitate.  Landy comments: In order to be enthralled, then, audience members did not have to believe Robert-Houdin possessed of mystical powers, or even particularly skillful. They had only to believe in the mysteries of science. Perfectly mixing (1) the narrative context offered by Robert-Houdin at the beginning, (2) the prior knowledge of some rudiments of science and (3) the perfect execution of the experiment (which included the use of scented bottles, smelling of ether), the illusion was impeccable. Somehow, the French magician showed that, presented in the right way, the same science “used” by Enlightenment to disenchant the world — discrediting religion and superstition — was able to re-enchant it, successfully evoking a sense of wonder. Landy summarizes it by writing: Performers like Robert-Houdin, even as they demystified old superstitions, were simultaneously replacing these with new sources of enchantment — indeed disenchanting by re-enchanting. But there is more. The French prestidigitateur did not contribute to the re-enchantment of the world through science, but through an illusion of science; we must keep in mind that in his flasks there was no ether, but a colored essence just imitating it, nor the levitation was really produced by a chemical. He said to use a science (ether) but used another (which one? Secret!) — and the spell emerged from this fundamental gap. It is the same with modern mentalists: they say to use a science (NLP) but use another (which one? Secret!) — and the spell emerges. The ideal audience of Robert-Houdin had to develop sophisticated skill: to be deceived in a voluntary and conscious way. Too religious individuals (who attributed magical effects to the Devil) missed such an ability, but also those with a inadequate scientific background (actually attributing the levitation to Ether) and the cynical/militant skeptics (who labeled his performances as insults to intelligence). Landy adds that Only those spectators who, with a mental agility equal to his manual dexterity, were ready to don and doff their lucidity repeatedly throughout the show, could respond appropriately to the Ethereal Suspension. [...] What Robert-Houdin required was, so to speak, an ethereal suspension of disbelief. Aiming to shape this kind of reaction in the audience, with a true emancipatory attitude, the magician could provide valuable stimuli: his shows were opportunities to hone a detached credulity — an attitude that could be extended to daily life, re-enchanting it in its entirety. Landy called the ethereal suspension “a model for the construction of a belief system that recognizes itself as illusory”. From the point of view of the magician, it requires a lot of efforts to maintain intermediate positions, but the price paid for emancipating the audience is fully paid off by the responses of the spectators. (3) In his best selling book Sum neuroscientist David Eagleman wrote about a fascinating intermediate philosophical position, lying between faith and agnosticism. Describing himself as “possibilist,” Eagleman does not adhere to any specific religious faith — admitting that he lacks sufficient rational data to choose one or the other. This lack, which leads the agnostic to stop and suspend judgment, is not an obstacle for him: possibilists deem interesting to cultivate multiple hypotheses about the nature of the transcendent, in a creative game that fully embodies the “detached credulity.” Eagleman’s stories staged in 40 possible afterlives literally ooze irony — the key ingredient to ease in the reader a healthy detachment. Citing Friedrich Schiller, the Nobel prize-winner Orhan Pamuk labels the two categories “Naive” and “Sentimental” readers — the first unaware of the existence of tricks behind the curtain, the second lacking the ability to enjoy the illusion. I prefer the two labels used in professional wrestling, with the same meaning — “Mark” and “Smart”. Each artist can actively adopt an emancipatory attitude towards her audience, refusing the dicotomy and aiming at a “Smark” reaction. Shaping in the audience the sophisticated skill of “detached credulity” is the most ambitious challenge for a modern magician.  _________________ (1) Joshua Landy, “Modern Magic: Jean-Eugène Robert-Houdin and Stéphane Mallarmé” in Joshua Landy and Michael Saler, The Re-Enchantment of the World: Secular Magic in a Rational Age, Stanford University Press, Stanford, 2009. (3) Among modern illusionists, the best attempts in pursuing detached credulity are the ones by Penn&Teller, Max Maven and Derren Brown. Magic & Transmedial spin-offMy magic celebration of the TV series Lost Posted on thursday 26 june 2014, 43 days before scifoo14 • Written by Mariano TomatisOn defining fandom, Henry Jenkins wrote that it is born of a balance between fascination and frustration: if media content didn’t fascinate us, there would be no desire to engage with it; but if it didn’t frustrate us on some level, there would be no drive to rewrite or remake it. (1) Lost in Lost, I deeply experienced both the sensations when watching at the celebrated TV series created by J.J. Abrams and Damon Lindelof. My will to participate in the narrative led me to the creation of a transmedial spin-off adding a “magical twist” to the story. My website dharmainitiative.it provided the fictional context for 5 web episodes, mixing orthodox elements — i.e. coherent with the original series — and original ones (listen to the introductory audio).  dharmainitiative.it is still available. According to the website, I had been appointed Chairman of “Mathematical Forecasting Initiative”, an organization featured in the series doing researches about the Mathematics of the Paranormal, Sacred Geometries, the role of Numbers in Magic and bizarre connections between Numerical Structures and Reality. My (actual) interest in the topic had led former Chairman’s widow to put in my hands all of the files belonged to her husband. Files included some (pretty damaged) 8 mm films presenting interactive experiments involving the viewers. Although audio tracks were missing, complete scripts of the experiments were available. The video (actually created by me) were presented as the restoration of the original footages with additional subtitles. In order to create the videos I have mixed some scenes from the TV series and original material edited by me. Inspired to the amazing Max Maven’s Mindgames (1984) — the first example of interactive magic in video — the five episodes were born at the intersection between magic and my favourite TV series. An act of love, sprung from the balance between fascination and frustration. The five episodes ★ Order and Chaos — Interactive Test #5 ★ Mathematics and Meteorology — Interactive Test #8 _________________ (1) Henry Jenkins, Convergence Culture: Where Old and New Media Collide, New York University Press, 2006, p. 247. Magic & Scientific DiscoveriesThe man who (didn’t) walk across the river Seine Posted on wednesday 25 june 2014, 44 days before scifoo14 • Written by Mariano TomatisThe philosopher and magician Martin Gardner once wrote: Just as knowing how a magic trick is done spoils all its wonder, so let us be grateful that wherever Science and Reason turn they plunge finally into stygian darkness. (1) Since Science borders with Magic, exploring its boundaries may be extremely risky. Commenting on one of the most funny blunder of 18th century, Robert Darnton asked: Man had just conquered the air; why could he not walk on water? What limits could be set to the invisible powers at the command of his reason? (2) On 25 June 2011 the British magician Steven Frayne, best known for his TV appearnces on the show Dynamo: Mission Impossible, has been seen walking across the river Thames. Many have compared Dynamo’s stunt to Jesus’ miracle (Matthew 14:22-33; Mark 6:45-52; John 6:15-21) but not many know that an engraving dated 1783 shows a similar scene; set in Paris, it represents a man walking across the river Seine.  Left: Dynamo on Daily Mail (2011). Perhaps he is an ancestor of Dynamo, because he signs with the letter D. We know little about him. He is a watchmaker from Lyon, but we remember him for an amazing invention: the elastic shoes for walking on water. The idea came to him looking a mechanical little doll and throwing stones on the surface of a river. On 8 December 1783 he announced the discovery in the Journal de Paris (3).   Lyon, December 1783. […] My discovery […] is the result of 20 years of work and expense. I’m flattered to have found the sure-fire way to walk with my feet dry on the surface of the water. I have discovered this looking at one of those mechanical rotating dolls that move thanks to a spring. Starting from the simplicity of this mechanism, I combined it with the principle that makes stones bouncing on the water of a river, concluding that it was possible to combine the two forces progressively, so that the resultant is able to support a weight more or less significant depending on its speed; with a motion proportional to the weight you can hold a solid object in equilibrium above a fluid. From these conjectures, I worked with the trust in the possibility of successfully implementing it, then achieving results which would not fail to arouse amazement and offer something revolutionary. I propose to traverse the length and breadth of the Seine without getting wet shoes, and to accomplish the feat multiple times on 1 January 1784 under the Pont-Neuf in Paris; but only if I will find on the other side, at the end of my journey, two hundred Louis with which to finance the trip. I am not going to exploit any other contraption except for a pair of elastic shoes, distant from one another no more than a normal step, fixed with a bar as two copper spheres. Each shoe, a foot long, will be 7 inches wide and high; with a pair of shoes like that, I can cross the wider river even 50 times in an hour. The curiosity and love for the arts and the public good will certainly encourage an adequate number of people in funding the amount of money requested, without which I can not perform the stunt. […] Signed: D…, watchmaker.  The Journal de Paris acts as guarantor for the collection of the money needed (200 Louis or the equivalent figure for 4800 livres) and in two days more than 1800 livres are collected.  Subscription report from Journal de Paris, 11.12.1783, p. 1416. On December 13, money raise to 3243 livres and among donors there is also the famous Marquis de La Fayette, who pays 48 pounds (equal to 2 Luigi, 1% of the total).  Subscription report from Journal de Paris, 11.12.1783, pp. 1436-1437. On December 18, the Journal involves the subscribers in the choice for the place from which they will watch “the spectacle of a man walking on the water” and explains that the tickets will be distributed to regulate access to the area. (4) In the meantime, P. Sellier is commissioned to create an artistic engraving of the event (5), to be offered to those who have subscribed. He imagines the scene like this: 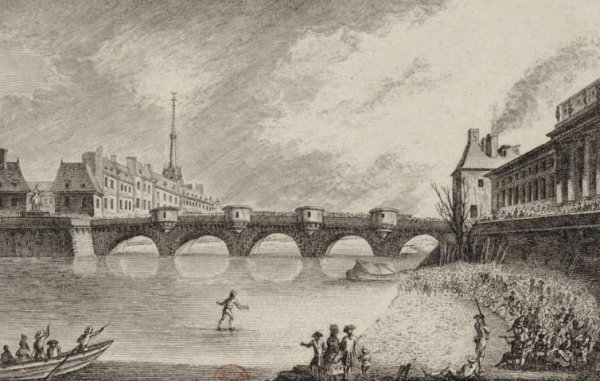 On 22 December, the daily journal takes a step back: Monsieur De Combles, the intermediary of the watchmaker, is increasingly vague and the correspondence with him becomes every day more suspicious; the existence of Mr. D. comes to doubt, and in a letter he declares that his name was Luc (but is he writing?). According to the Journal there is enough to stop the subscription: since it is most likely a hoax, who has paid the sums is asked to return to get it back. (6) Two days later, the paper confirms that it was a sham, adding that many readers have preferred to leave the money to charities. (7) But the imagination of the artists has already been tickled, and before discovering the hoax, circulating engravings herald the scene — imagining that the protagonist will support himself with two small balloons.  Even the Magasin Pittoresque dedicates to the event a portrait in action. (8)  Robert Darnton will comment: The burst of enthusiasm for the project, the imposing names on the list of subscribers, and the lack of precautions taken by the journal pointed to the same attitude. […] By February 7 [the journal] had overcome its embarassment well enough to print a letter promoting a technique for seeing in the dark, which was sponsored by a club of balloon enthusiasts convinced of the brotherhood of “nyctalopes, hydrophobes, somnambulists and water witchers.” (9)  _________________ (1) Martin Gardner, The Whys of a Philosophical Scrivener, St. Martin Griffin, New York 1999, p. 341. (2) Robert Darnton, Mesmerism and the End of the Enlightenment in France, Harvard University Press, 2009, pp. 23-24. (3) Journal de Paris, 8.12.1783, pp. 1404-1405. (4) Journal de Paris, 18.12.1783, p. 1448. (5) The engraving will be described as extremely rare in La Revue universelle des arts, t. IV, marzo 1857, pp. 544-547. (6) Journal de Paris, 22.12.1783, pp. 1465-1467. (7) Journal de Paris, 24.12.1783, pp. 1474-1475. (8) Magasin pittoresque, t. XIX, 1851, p. 273. (9) Robert Darnton, Mesmerism and the End of the Enlightenment in France, Harvard University Press, 2009, pp. 23-24. |
 Science Foo Camp (or “Sci Foo”) is an invitation-only gathering organized by Digital Science, O'Reilly Media, and Google, with support from Nature. The 9th edition of Sci Foo takes place on 8-10 August 2014 at the Googleplex in Mountain View, CA. Lord Martin Rees has defined it as “a sort of mini Woodstock of the Mind”. Participants include researchers, writers, educators, artists, policy makers, investors, and other thought leaders, all doing groundbreaking work in diverse areas of science and technology.
Science Foo Camp (or “Sci Foo”) is an invitation-only gathering organized by Digital Science, O'Reilly Media, and Google, with support from Nature. The 9th edition of Sci Foo takes place on 8-10 August 2014 at the Googleplex in Mountain View, CA. Lord Martin Rees has defined it as “a sort of mini Woodstock of the Mind”. Participants include researchers, writers, educators, artists, policy makers, investors, and other thought leaders, all doing groundbreaking work in diverse areas of science and technology.