MARIANO TOMATIS

Magic can be used in school to stimulate students’ curiosity. Are you a math (or computer science) educator willing to involve your students in a magic trick with educational purposes?

With the material here provided you will entertain your students for a few hours with a non-trivial mathematical analysis, kicking off with a magic trick.

Each student needs these 7 playing cards:

They can easily create them with a crayon and some pieces of paper.

Premise

Since the 19th century, mathematics has supported criminology to capture criminals. The French Ravachol (1859-1892) has been one of the most famous bandits caught with a mathematical model, invented by Alphonse Bertillon (1853-1914). The bomber became so famous that even today, in France, the verb “to ravachol” means “to blow up”. Is it theoretically possible to locate a mathematical scheme in seemingly random movements of a terrorist?

Please take part to this story putting your cards in front of you and following the instructions provided. You will be amazed!

Reaction

The repeated shuffles leads us to think that the “Black Knight” is totally lost in the deck. The pleasure springs out when the video is able to guess where Ravachol is. The absence of a magician in flesh and bones excludes the possibility of sleight of hand and leaves us puzzled. Nothing encourages a deeper analysis during the story, we are not told in advance what to expect, so we are left without a rational explanation about what happened.

The wonder lasts only a moment. Quickly our brain regains control of the situation — but a certain intellectual effort is needed to put what happened in the correct, rational perspective. In that special moment, we are spontaneously triggered to start a deeper analysis of the topic. When the students are involved, wonder has lit a spark, and even without explicitly invite them to do so, they have already started to meditate upon what may be behind the curtain.

For many, the urge to “fix” the cognitive dissonance arises from the discomfort of being deceived, and the impulse to prove — to themselves and to others — that are not naive. Best magicians are well aware of this dynamic, and they work against such an interpretation, shaping narratives which exclude the idea of ​​a challenge to the intelligence of the spectator. In contrast, a teacher can direct the same energy towards the exploration of very interesting mathematical mechanisms.

Observation, Hypothesis and Experiment

This magic trick forces the student to follow spontaneously the different stages characterizing the Scientific Method. The Observation (of the mysterious phenomenon) is followed by the formulation of a Hypothesis. You can invite students to suggest some possible explanations, and in all likelihood one of the first hypotheses will be the correct one: the special cards stays 5th position, regardless of the number of shuffles made.

The formulation of the hypothesis can be followed by the actual Experiment. Students can test the hypothesis with cards in their hands, discovering that indeed the position of the special card is invariant with respect to the repeated suffles; such verification is easier when the special card is face up in the face down deck.

A few tests will be enough to confirm the hypothesis (and some students may also sense that this counterintuitive knowledge will enable them to amaze their friends with 7 ungaffed playing cards.)

The study of a function

After their meeting with the abstract concept of “invariance”, it is time to suggest the students some ways to go deeper in the exploration. You can do this with a question: “Is the 5th card the only one that never changes position?”

The answer is far from obvious, and to verify it demands some investigation. A “brute force” approach is to shuffle the deck keeping an eye on the 1st card, checking if it does change position. Given that the cards “moves” from its position, the shuffle can be repeated keeping an eye on the 2nd card and so on — until having explored all the 7 cards.

When the answer is found, you can invite them to represent graphically the results of their investigation. This step is crucial, because a graph summarizes — in a single glance — all the information gathered during the analysis.

You can invite your students to use a grid like this:

Each line corresponds to the position of a card in the DECK. The vertical divisions correspond to the shuffles. In order to keep track of the 1♥ through the deck, the students must start from the top in the upper left. The 1st shuffle moves the card from the first to the last position, so they draw a sloping red line to the bottom line, at the intersection with the vertical line separating the first two shuffles. A 2nd distribution will move the 1♥ from last to 4th position, and then the red line should be traced to the right going up to the 4th line. Proceeding in this way, the card will return to the first position after the 6th distribution. Here is the resulting graph: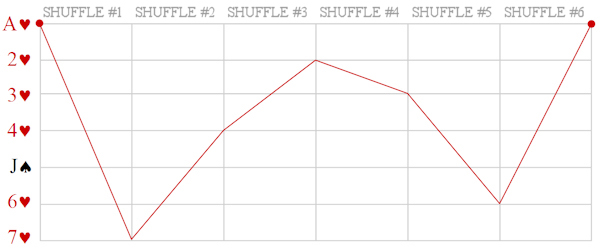

You can point out that the graph is complete, and covers the entire history of the card, even for a larger number of mixtures: since the card returns to the first position, the graph drawn by the students is cyclical; if the 1♥ is in 4th position after 2 shuffles, it will be in the same position after 2 + 6 = 8 suffles, 2 + 6 + 6 = 14 suffles and so on. The “frequency” of the route through the deck is equal to 6.

The graph can be plotted for each card — and of course the most interesting is the one of the J♠ which is completely flat:

Superimposing the graphs, the “singularity” of the J♠ (and its invariant position) is immediately clear and doesn’t need any additional explanation: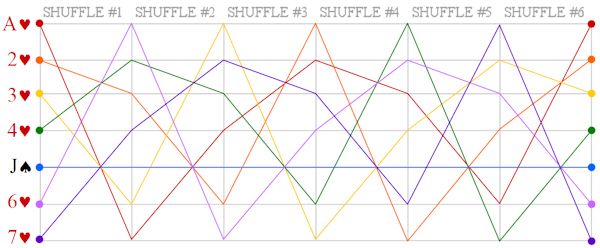

Another interesting point is that the route taken by the six “moving” cards is the same: if a card is in the first position, after the next shuffle will end up in last place, regardless of how many shuffles have been made so far; the different routes are simply shifted one to another.

After drawing the graphs, the students should grasp the fact that the shuffle is nothing more than a function operating on the positions of each card, commuting them in a predictable way. Mathematically, the function is applied to a vector of seven elements and returns a vector with the same elements scrambled.

Intuitively, it may be represented by a series of tubes with seven balls: with the exception of the fifth one, passing through the tubes the balls change their relative positions.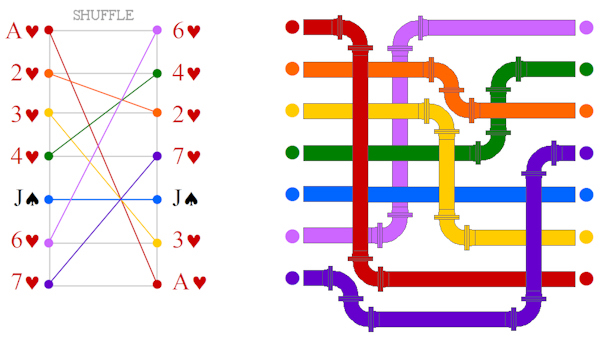

To study the effect of two shuffles is to apply twice the function to the starting vector — or more easily, to put two series of identical tubes and see the effect on the balls through them:

The cyclical nature of the function is highlighted by applying it six times, getting the starting vector as a result.

Combining six tube-structures, we would build this unlikely (and totally useless) machinery, keeping all the balls in the same order!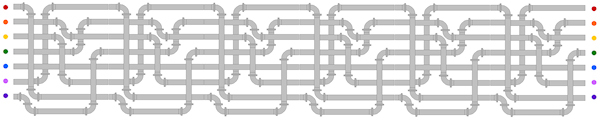

At this point the students should be particularly amazed by the idea of ​​studying a function using a deck of playing cards.

Further questions

In order to show them the width of the mathematical universe that has opened up before their eyes, some interesting questions may suggest new creative ideas:

• What if, after the distribution of the two groups of card on the table, you put the smaller over the bigger? Is there a fixed card also with this new distribution? What is its graph? Which is the lenght of its cycle?

• What if the deck is composed of an odd number of cards other than 7? In this case, we must distinguish between the shuffle completed by putting the smaller group over the larger, and the one in which the larger is placed on the smaller.

• Even more difficult: what if the deck is composed of an even number of cards?

A fascinating side of the mathematical area addressed here is the existence of a large number of open questions; it is a point to emphasize, because it enables the students to live the experience of being pioneers in an unexplored region.

• A bunch of 3 cards has no invariant card, but a bunch of 5 or 7 card does have it. Is there a rule for predicting whether a deck consisting of 2N+1 cards has (or not) an invariant card?

• How can the shuffle be modified so that a deck of 3 cards present an invariant? How can you do the same with a generic deck of 2N+1 cards?

• A deck of 5 cards has a 4-shuffles cycle; a 7 card has a 6-shuffles cycle. Is there a rule to calculate the length of the cycle of a deck of 2N+1 cards?

• How can you change the shuffle so that there is more than an invariant card?

The study of these questions will lead, spontaneously, to address deeper issues and to the construction of a broader theory of vectorial functions applied to playing cards.