MARIANO TOMATISWONDER INJECTORScrittore e illusionista
|
 Giocare con il Libro di Soyga - 1 Pubblicato lunedì 30 aprile 2012 • Scritto da Mariano Tomatis • PermalinkIl Libro di Soyga è uno strano trattato magico del Cinquecento composto da 36 tavole piene di lettere indecifrabili. Recentemente James A. Reeds ha scoperto la regola matematica con cui è stato compilato, a partire da 36 "parole magiche". La stessa norma può essere usata per divertenti attività ludiche. Prima di leggere questo post, scopri qui la storia del libro e le regole per realizzarlo. Un libro magico del Cinquecento può essere usato per interessanti esplorazioni enigmistiche e matematiche. La disposizione delle lettere sulle sue 36 tavole è solo apparentemente casuale: studiarne le regolarità non richiede conoscenze di matematica superiore, e rivela dettagli curiosi. Ecco una prima domanda interessante: È possibile, agendo sulla "parola magica" che genera ogni tavola, creare parole di senso compiuto all’interno della tavola stessa? Per scoprirlo, soffermiamoci sulla prima riga in alto. 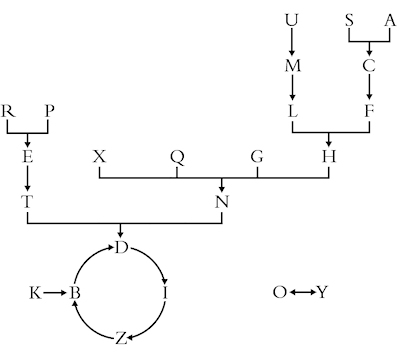La prima riga La regola matematica per compilare la prima riga può essere condensata in questo grafico:  La regola che determina la successione di lettere sulla prima riga di una tavola di Soyga Da ogni lettera parte una e una sola freccia. Poiché una freccia porta dalla U alla M, sulla prima riga di una tavola di Soyga a destra di ogni U comparirà una M. Iterativamente, poiché una freccia collega la M e la L, a destra della M comparirà sempre e soltanto la L. Fissata liberamente la prima lettera a sinistra, tutte le successive sono determinate una volta per tutte dalla regola. La prima tavola si apre con la lettera N. Seguendo la freccia, la lettera successiva è la D. A questo punto il percorso si chiude in un circolo, che tocca in successione le lettere D/I/Z/B. Dunque la prima riga della prima tavola sarà una N seguita dalle lettere DIZB che si ripetono identiche all’infinito.  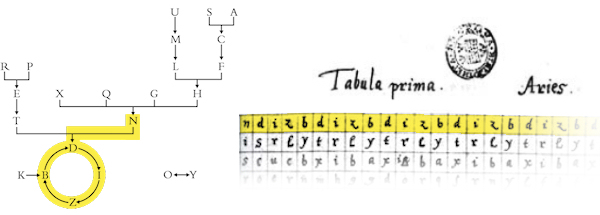In giallo è evidenziato il percorso che porta alla definizione della prima riga della prima tavola di Soyga. Osservando il grafico della regola si nota che qualsiasi lettera conduce al fatidico ciclo - a eccezione delle lettere O e Y; queste due danno vita a un ciclo più piccolo, in cui si alternano senza fine (ciò accade, ad esempio, sulla quinta tavola del Libro di Soyga, la cui prima lettera è una O). Nella teoria del caos le sequenze DIZB e OY si chiamerebbero attrattori (1), perché sembrano "attrarre" i percorsi come farebbe un buco nero; per questo motivo Michael W. Ecker preferisce chiamarli "buchi neri matematici". (2) L’esistenza dei due attrattori rende impraticabile l’idea di agire sulla prima lettera per produrre parole di senso compiuto sulla prima riga: qualsiasi lettera si scelga, la sequenza è destinata, nel giro di pochi passi, a collassare sulla sequenza DIZBDIZBDIZB... Le righe successive sono altrettanto "noiose"? Clicca qui per accedere alla seconda puntata _________________ (1) Alexander K. Dewdney, "Probing the Strange Attractors of Chaos", Scientific American, Vol. 257, p. 108, luglio 1987. (2) Michael W. Ecker, "Number play, calculators, and card tricks: Mathemagical black holes" in E. Berlekamp e T. Rodgers (edd.) The Mathemagician and Pied Puzzler: A Collection in Tribute to Martin Gardner, A K Peters, Natick (MA, USA). L’articolo si può scaricare da qui. Potrebbero interessarti anche:
|
