Il 18 giugno 1964 Juanita Brooks fu scippata. Qualcuno la buttò per terra tirando la borsa, e lei vide con la coda dell’occhio una ragazza bionda che scappava. Interrogata dalla polizia, la donna raccontò di aver notato che la giovane portava la coda di cavallo ed era fuggita su un’auto gialla, guidata da un nero con la barba e i baffi.
Pochi giorni dopo, Janet e Malcolm Collins furono arrestati e processati perché il loro aspetto era identico a quello descritto da Juanita. In tribunale, le ragioni dell’accusa furono affidate a un docente di matematica, che usò senza ritegno quella che in tribunale si chiama fallacia dell’accusatore. L’uomo scrisse su una lavagna questa tabella:
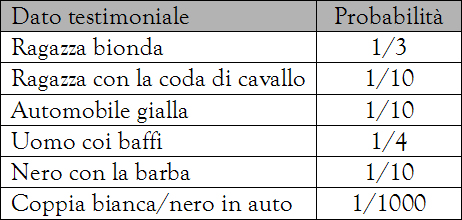
Secondo l’insegnante, ci si doveva chiedere: qual è la probabilità che i coniugi Collins siano innocenti se hanno tutte le sei caratteristiche elencate sulla lavagna?
Dal punto di vista matematico, la probabilità congiunta di svariate caratteristiche si ottiene moltiplicando tra loro tutte le singole probabilità. Calcolando il prodotto delle sei frazioni riportate nella tabella, l’esperto spiegò che se si prende una coppia qualsiasi, solo una su 12 milioni possiede le stesse caratteristiche. Quindi, concluse, la probabilità che i Collins siano innocenti è di 1 su 12 milioni.
La giuria ritenne convincente l’argomento, e condannò la coppia per rapina.
La difesa si appellò alla sentenza, e la Corte Suprema della California individuò la fallacia del ragionamento, denunciandola apertamente: la tabella consentiva di concludere soltanto che “ogni 12 milioni di coppie si può prevedere che una presenti queste sei caratteristiche.”
Usando come riferimento le 24 milioni di coppie che vivono in California, la Corte calcolò che esistono almeno due coppie che corrispondono alla testimonianza di Juanita Brooks... ma solo una è colpevole di scippo! La sentenza di appello concluse che la condanna dei Collins era paragonabile alla condanna di una persona sulla base del fatto che un testimone aveva visto lei – o il suo fratello gemello – commettere il crimine; in assenza di altri indizi, la certezza di una colpevolezza oltre ogni ragionevole dubbio non si poteva dire raggiunta. Denunciando l’uso della fallacia da parte dell’accusa, i giudici della Corte spiegarono che si trattava di una buccia di banana su cui era facile scivolare:
Era prevedibile che pochi avvocati difensori, e sicuramente pochi giurati, si rendessero conto di questo fondamentale difetto dell’analisi dell’accusa.
Eppure si tratta di una fallacia riproposta di continuo. Perfino per “dimostrare” che la Sindone è autentica.
Il principale obiettivo della “sindonologia” è di risolvere un caso di carattere criminologico: a chi appartiene l’impronta sulla Sindone di Torino? Come se si trattasse di un corpo sulla scena del crimine, l’immagine è stata studiata da medici legali, biologi, chimici, fisici, esperti di pollini – ma anche da storici dell’arte, fotografi, informatici… Il matematico Bruno Barberis ha proposto un contributo “numerico” in un articolo (1) dedicato al “calcolo delle probabilità applicato al problema dell’identificazione dell’Uomo della Sindone”. Come nel caso dei coniugi Collins, Barberis elenca alcune caratteristiche dell’impronta sindonica, stimando la probabilità che si possano trovare sul cadavere di una persona qualsiasi:

Barberis spiega che, per valutare la probabilità che i sette eventi si siano verificati contemporaneamente, bisogna moltiplicare tra loro le sette singole probabilità. Il prodotto fa 1 su 200 miliardi, e il matematico torinese commenta:
Poiché anche nel caso di Gesù […] si sono verificate le sette caratteristiche qui prese in considerazione, possiamo concludere che è altissima la probabilità che l’uomo della Sindone sia Gesù di Nazaret.
Ma è di nuovo in gioco la fallacia dell’accusatore: in tribunale, la piccola probabilità di una corrispondenza casuale veniva scambiata per la probabilità di essere innocenti; qui l’esigua probabilità di una corrispondenza casuale con le caratteristiche della Sindone viene confusa con la probabilità che la Sindone sia un falso: le due questioni, però, non hanno nessuna relazione reciproca.
Osservando l’uomo sorretto dalla Madonna nella Pietà di Michelangelo, potremmo interrogarci sulla probabilità che un cadavere qualsiasi sia stato crocifisso, mostri le stesse ferite ai polsi, ai piedi e al costato, ecc. Moltiplicando le singole frazioni, otterremmo una probabilità infinitesima, concludendo trionfanti – con Bruno Barberis – che è altissima la probabilità che l’uomo scolpito da Michelangelo sia Gesù di Nazareth. Ma c’era bisogno di probabilità composte per dimostrare le intenzioni dello scultore?
Se la Sindone è un falso medievale, il matematico torinese non fa che dimostrare l’intento del suo falsario: rappresentare il corpo di Cristo e presentare il telo come autentico.
Tutti i post sono distribuiti con Licenza Creative Commons BY-NC-SA 4.0